概率極低的事件(對稀有事件數據分析的討論)
在社會科學的數據分析中,有那么一類變量比較常見,即0-1的二分變量。當它是自變量時,則稱為虛擬變量回歸模型,當它是因變量時,此時常用的模型是logistic或probit回歸(這兩種模型的區別在于對方差的假定不同,二者估計的結果差異不大,但是在更為復雜的模型中可能會有不同的功能)。二分變量可以詮釋為有或無,發生或沒有發生等。在流行病學或社會科學中,有一些事件會發生,但是出現的頻次比較低,比如戰爭、罕見病癥以及政體變遷等。很多時候定性研究在這種重要的罕見事情上大放光彩,通過深入的資料檔案分析與小案例比較方法來探究這些事件的成因,總結出具有一定普適性的理論。
在定量研究中,稀有事件的logistic分析往往存在困難,這點在數學上可以解釋,即頻率派方法求解待估計系數矩陣時(公式如下),如果事件發生概率過低,矩陣中就會有很多元素約等于0,那么在求矩陣的逆矩陣時就容易出問題,造成估計結果的可信度不高。現在的問題是:什么樣的數據算是稀有事件數據?
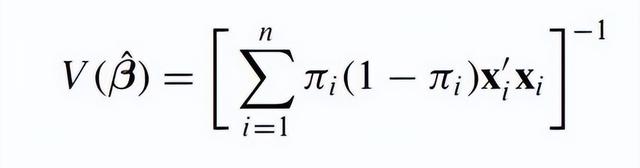
加里·金(Gary King)2000年左右與其合作者發表的兩篇文章討論了對稀有事件回歸模型的估計修正。當然,他們也沒有指出多小的比例算是稀有事件(不過他們文章中使用的數據集比例是0.34%,的確算比較小了)。他們文章的核心觀點是,通過先驗調整(prior correction)或者加權(weighting)的方式來調整估計系數使得樣本估計更接近總體。核心的參數是樣本的稀有事件比例和總體的稀少事件比例。因為他們認為稀有事件數據在數據收集過程中會面臨樣本量和變量數目的權衡,因此在估計上可能會低估了稀少事件的出現頻次,因此這個調整方案目的和功能也只是讓估計更接近真實參數而非優化估計。
那么核心問題是,多少比例的稀有事件才需要修正呢?為此小編采用仿真模擬(simulation)的方法,構建了不同比例的稀少事件數據集,分別使用普通的logistic方法和Gary King的rare event logit方法來得到解答。數據分析使用R,基礎包的glm()函數提供了logistic回歸的程序,Zelig包中的relogit()函數提供了rare event logit的程序(這個包的其他函數出了問題,近期剛剛下架,但是錯誤報告里面沒有提relogit()的問題,因此可以用之前版本的進行計算)。
小編設定了從0.001到0.01的以0.001為步長的比例值和從0.01到0.20的以0.01為步長的比例值,最終共得到29個比例值,分別看這兩種估計方法在不同稀少比例下的表現。由于logistic固定了常用閾值,因此設計陣xβ和比例p之間存在某種函數關系,這種函數關系沒有解析解,只能通過仿真方法求得數值解進行比較。這里小編還設定了隨機數種子666(希望獲得好運)使得結果可重復,并虛擬了100000個樣本量的數據集,變量服從最小值為0,最大值為10的均勻分布(正態分布最終會導致估計比例收斂到0.5,沒有辦法達到想要的比例)。下圖是仿真模擬的結果。
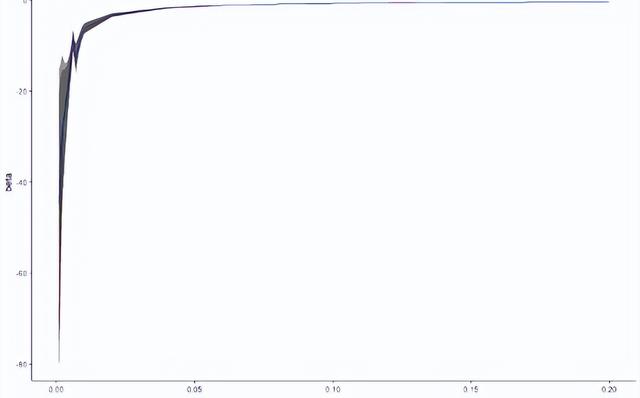
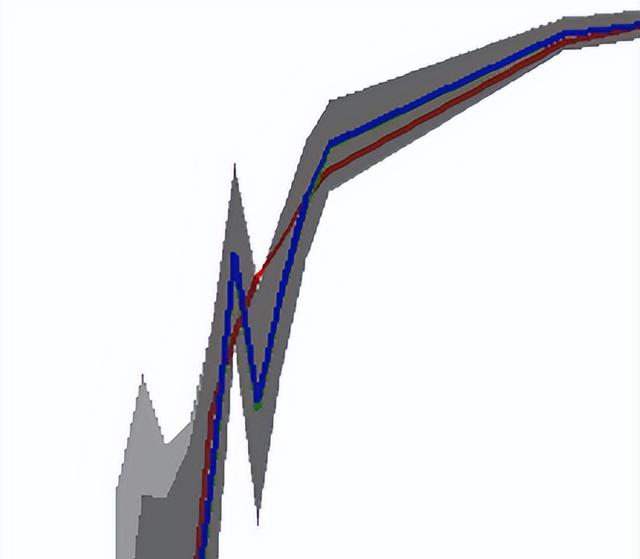
這幅圖展示的是給定數據集的β和比例p之間的真實關系(紅線)、logit回歸的估計(綠線),rare event logit回歸的估計(藍線)。為了看得更清晰,截取上左圖的部分結果放到右圖,可以看到盡管估計上有差異,但是由于關鍵回歸系數的標準誤巨大,因此真實值也依然在估計的不確定范圍(uncertainty)內。為了進一步觀察,小編計算了估計值和真實值之間的差異占真實值的比例,結果如下圖。
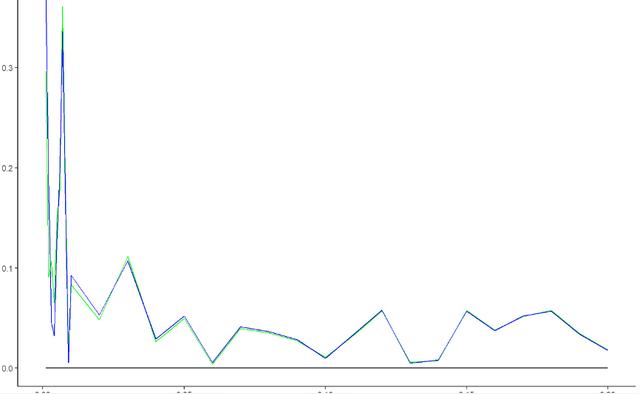
這張圖我們大概可以看出來,當p比較小的時候,估計值和真實值的差異非常大。而且更為關鍵的是,rare event logit表現也沒比正常的回歸方法要好到哪里去。所以至少目前的仿真模擬結果呈現出來的結果是,如果以偏差10%為標準,至少比例要達到1%,如果稀有事件數據比例低于1%,兩種方法估計上比較不出誰優誰劣。
所以目前能夠初步得出的(未經系統檢驗的)結論是,如果稀有數據的比例達到1%,那么logit模型一般不會有非常大的估計偏差(形象地想一下,如果有3000個樣本量的觀測,某個二分變量只有30個不到的1,是不是很多人都有選擇扔掉的沖動)。低于該比例的,目前尚無可信的估計方法。當然,小編也嘗試了一下貝葉斯(Bayesian)方法,貝葉斯給出的結果同樣有比較偏離的估計和較大的可信區間,由于一次貝葉斯估計的時間過長,因此小編沒有把所有29個比例全部跑完。此外,貝葉斯的結果也取決于先驗(prior)的設定,如果先驗設定得好那擬合就非常棒,但是現實的結果是,我們并不知道待估計參數的真實值,即使將普通回歸的結果作為一個弱先驗給貝葉斯也沒有明顯的改善。不過這種仿真模擬還比較簡單的,其中可能存在一些因個人水平有限而沒有意識到的問題與錯誤,如果有愿意討論的師友想要進一步討論,還望不吝賜教!
撰文:劉天祥
